너비 우선 탐색 Depth First Search(DFS)

이 글은 제 개인적인 공부를 위해 작성한 글입니다.
틀린 내용이 있을 수 있고, 피드백은 환영합니다.

개요

---

• 너비 우선 탐색(BFS, Breath First Search)은 그래프 탐색 방법 중 하나이다.
• 특정 노드에서 시작해서 인접한 노드를 먼저 탐색하는 방법이다.
• 두 노드 사이의 최단 경로 혹은 임의의 경로를 찾고 싶을 때 BFS를 사용할 수 있다.
• 큐를 이용하여 구현한다.
• BFS는 재귀적으로 동작하지 않는다.
• 장점
  • 시작 노드에서 목표 노드까지 최단 길이를 보장한다.
• 단점
  • 노드와 연결된 모든 노드들을 큐에 집어넣어 메모리 소모가 크기에, 입력이 큰 경우 DFS를 사용하는 것이 좋다.
  • 해가 없다면 유한 그래프의 경우, 모든 그래프를 탐색한 후에 실패로 끝난다. 무한 그래프의 경우에는 해도 못 찾고, 끝내지도 못한다.

과정

---

1. 탐색을 시작할 노드를 방문하고, 큐에 넣은 후 방문했음을 표시한다.
2. 큐의 가장 앞에 있는 노드를 꺼낸다.
3. 꺼낸 노드의 인접한 노드들 중 아직 방문하지 않는 노드들을 모두 찾아 큐에 넣고 방문했음을 표시한다.
4. 큐가 빌 때까지 이 과정을 반복한다.

시간복잡도

---

• 인접 행렬 : $O(n^2)$
• 인접 리스트 : $O(n+e)$

구현

---

void bfs(int startNode, 
         std::vector<std::vector<int>>& adj, 
         std::vector<bool>& visited) 
{
    std::queue<int> q;

    q.push(startNode);
    visited[startNode] = true;

    while (!q.empty()) 
    {
        int node = q.front();
        q.pop();

        for (int neighbor : adj[node]) 
        {
            if (!visited[neighbor]) 
            {
                visited[neighbor] = true;
                q.push(neighbor);
            }
        }
    }
}

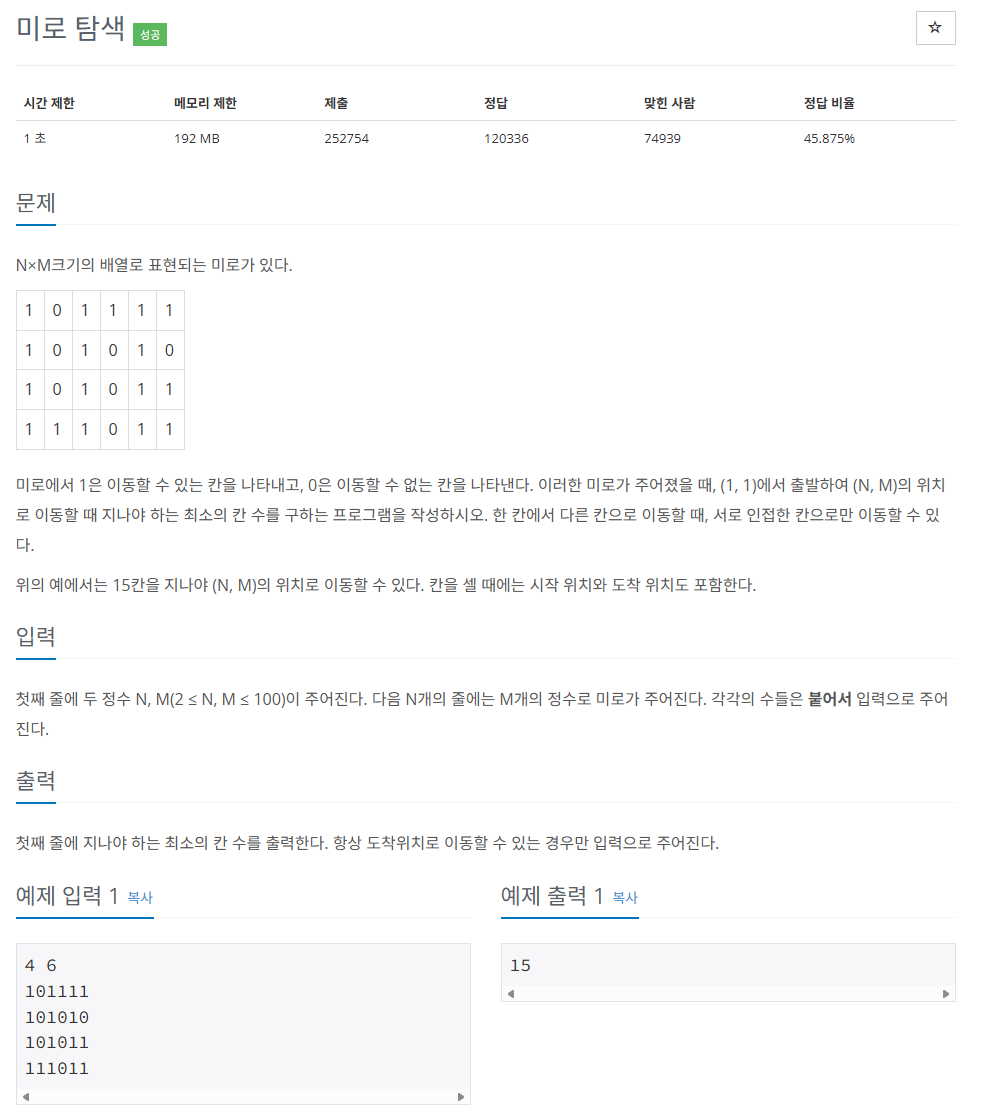
백준 2178번 : 미로 탐색

---

#include <iostream>
#include <vector>
#include <queue>

int n, m;
int dx[] = {0, 0, 1, -1};
int dy[] = {1, -1, 0, 0};

void bfs(int i, int j, std::vector<std::vector<int>>& adj, std::vector<std::vector<int>>& cnt) 
{
    std::queue<std::pair<int, int>> q;

    q.emplace(i, j);

    while (!q.empty()) 
    {
        int x = q.front().second;
        int y = q.front().first;
        q.pop();

        for (int d = 0; d < 4; d++)
        {
            int nx = x + dx[d];
            int ny = y + dy[d];

            if (nx < 0 || nx >= m || ny < 0 || ny >= n || adj[ny][nx] == 0 || cnt[ny][nx] != 0) continue;

            cnt[ny][nx] = cnt[y][x] + 1;
            q.emplace(ny, nx);
        }
    }
}

int main()
{
    std::ios_base::sync_with_stdio(false);
    std::cin.tie(nullptr);
    std::cout.tie(nullptr);

    std::cin >> n >> m;
    std::vector graph(n, std::vector<int>(m));
    std::vector cnt(n, std::vector(m, 0));
    cnt[0][0] = 1;

    for (int i = 0; i < n; i++)
    {
        std::string s;
        std::cin >> s;
        for (int j = 0; j < m; j++)
        {
            graph[i][j] = s[j] - '0';
        }
    }

    bfs(0, 0, graph, cnt);
    std::cout << cnt[n - 1][m - 1];
    
    return 0;
}