다익스트라 알고리즘 Dijkstra Algorithm

본 글은 제 개인적인 공부를 위해 작성한 글입니다. 틀린 내용이 있다면 언제든지 피드백을 주시면 감사하겠습니다. 참고로만 활용해주시길 바랍니다.

개요

---

하나의 정점에서 출발했을 때 다른 모든 정점으로의 최단 경로를 구하는 알고리즘

• 어떤 경로도 음수 가중치를 갖지 않는 그래프에서 사용 가능
• 유향/무향 상관이 없다.

다익스트라 알고리즘은 욕심쟁이 기법과 다이나믹 프로그래밍 속성을 모두 가지고 있다.

1. 욕심쟁이 기법

   매 순간 현재 위치에서 갈 수 있는 가장 가까운 노드를 선택하는 방식이다. 지금 당장 거리가 가장 짧은 노드를 방문하면, 그 노드까지의 최단 거리는 더 이상 바뀔 일이 없다. 한 번 최단 거리로 확정된 노드는 다시 계산하지 않고 그대로 넘어간다.

1. 다이나믹 프로그래밍

   알고리즘이 동작하는 구조를 보면 DP의 핵심 원리인 최적 부분 구조(Optimal Substructure)를 활용한다. 시작점부터 노드 C까지 가는 최단 거리는 ‘시작점 -> 노드 B까지의 최단 거리’ + 노드 B -> C 거리’의 합으로 이루어진다. 즉, 큰 문제의 해를 구하기 위해 부분 문제의 해를 활용한다. 또한, 각 노드까지의 최단 거리를 테이블에 기록해 두고, 새로운 경로를 발견할 때마다 기존 값과 비교하여 갱신하는 메모이제이션을 사용한다.

과정

---

1. 모든 노드의 거리를 큰 수로 초기화하고 시작 노드의 거리를 0으로 초기화
2. 아직 방문하지 않은 노드 중 가장 가중치가 작은 노드 방문
3. 해당 노드를 거쳐 갈 수 있는 노드의 거리가 이전보다 작으면 해당 거리를 갱신
4. 더 이상 방문할 노드가 없을 때까지 2~3 반복

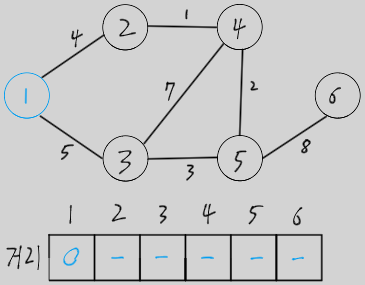모든 노드의 거리를 큰 수로 초기화하고, 시작 노드(1)의 거리를 0으로 초기화

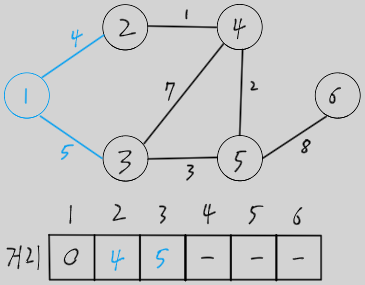시작 노드에서 갈 수 있는 노드들의 거리를 갱신 (현재 선택된 노드와 에지는 파란색으로 표시)

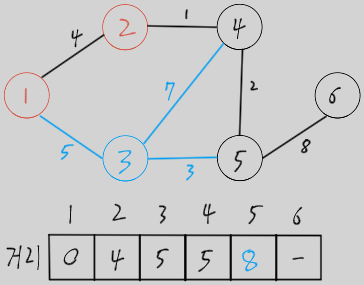
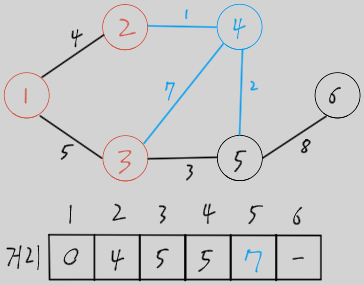
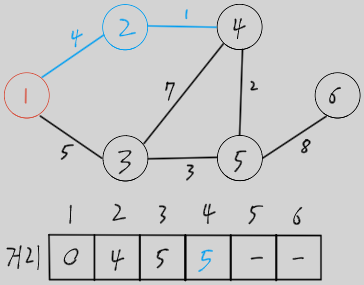아직 방문하지 않은 노드 중 가장 가중치가 작은 노드(2) 방문 및 해당 노드를 거쳐 갈 수 있는 거리 중 최단 거리가 있다면 갱신 (이미 방문한 노드는 빨간색으로 표시)

반복

반복

반복

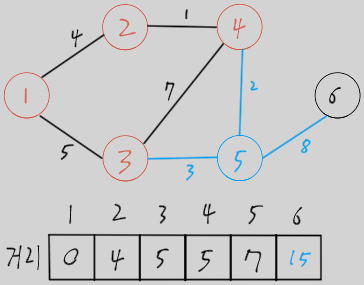
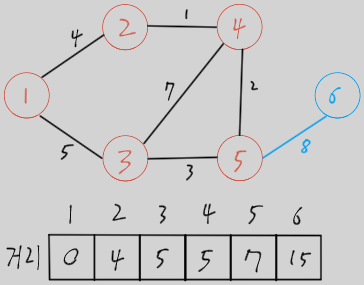더 이상 방문할 노드가 없고, 노드 1에서 모든 노드로 가는 최단 거리를 구하였음

시간 복잡도

---

$V$: 노드의 숫자, $E$: 간선의 숫자

초기 알고리즘의 시간 복잡도는 $O(V^2)$

• $V$ 크기의 최단거리 1차원 배열을 매번 반복문을 이용하여 검사
• 총 $O(V)$번에 걸쳐서 모든 인접노드를 검사하기에 $O(V^2)$

최소 힙(우선순위 큐)으로 구현 시 $O((V+E)log V)$

• $VlogV+ElogV=(V+E)logV$
• 각 노드마다 미방문 노드 중 출발점으로부터 현재까지 계산된 최단 거리를 가지는 노드를 찾는데 $O(VlogV)$
  • 최대 $V$개의 노드가 들어가 있는 우선순위 큐에서 삭제 연산 $(logV)$
• 각 노드마다 이웃한 노드의 최단거리를 갱신하는데 $O(ElogV)$
  • 각 노드에 연결된 최대 $E$개의 에지에서 우선순위 큐에 삽입 연산 $(logV)$

백준 11779번 : 최소 비용 구하기 2

---

https://www.acmicpc.net/problem/11779

#include <algorithm>
#include <iostream>
#include <vector>
#include <queue>
#include <climits>

struct node
{
    int end;
    int cost;
    
    node(const int inEnd, const int inCost) : end(inEnd), cost(inCost) {}
    
    bool operator<(const node& other) const
    {
        return cost > other.cost;
    }
};

int N, M;

void Dijkstra(std::vector<std::vector<node>>& graph, int start, int end)
{
    std::vector dist(N + 1, INT_MAX);
    dist[start] = 0;
    
    std::priority_queue<node> pq;
    pq.emplace(start, 0);
    
    std::vector backtracking(N + 1 , -1);
    
    while (!pq.empty())
    {
        auto [node, cost] = pq.top();
        pq.pop();
        
        if (dist[node] < cost) continue;
        
        for (auto& [adj_node, adj_cost] : graph[node])
        {
            if (dist[adj_node] > dist[node] + adj_cost)
            {
                dist[adj_node] = dist[node] + adj_cost;
                pq.emplace(adj_node, dist[adj_node]);
                
                backtracking[adj_node] = node;
            }
        }
    }
    
    std::vector<int> path;
    for (int i = end; i != -1; i = backtracking[i])
    {
        path.emplace_back(i);
    }
    std::reverse(path.begin(), path.end());
    
    std::cout << dist[end] << '\n' << path.size() << '\n';
    for (const auto& elem : path)
    {
        std::cout << elem << ' ';
    }
}

int main()
{
    std::ios_base::sync_with_stdio(false);
    std::cin.tie(nullptr);
    std::cout.tie(nullptr);
    
    std::cin >> N >> M;
    
    std::vector graph(N + 1, std::vector<node>());
    
    int s, e, c;
    for (int i = 0; i < M; i++)
    {
        std::cin >> s >> e >> c;
        graph[s].emplace_back(e, c);
    }
    
    int start, end;
    std::cin >> start >> end;
    
    Dijkstra(graph, start, end);

    return 0;
}

참고

• https://ko.wikipedia.org/wiki/데이크스트라_알고리즘
• https://infossm.github.io/blog/2019/01/09/wrong-dijkstra/