두 포인터 Two Pointer

이 글은 제 개인적인 공부를 위해 작성한 글입니다.
틀린 내용이 있을 수 있고, 피드백은 환영합니다.

개요

---

두 포인터는 리스트에서 두 개의 점의 위치를 기록하면서 처리하는 알고리즘이다.

배열의 부분 배열 중 그 원소들의 합을 구해야 하거나, 배열의 원소들 중에 몇 개의 합이 특정 수가 되는 가짓수를 구할 때 유용하다.

과정

---

간단한 백준 문제로 알아보자.

https://www.acmicpc.net/problem/3273

5 12 7 10 9 1 2 3 11 라는 수열이 있을 때, 어떤 두 수의 합이 13이 되는 경우의 수를 구하는 문제이다.

단순히 이중 반복문을 사용하면 O(N^2)의 시간 복잡도가 걸리지만, 두 포인터를 사용하면 O(N log N)의 시간 복잡도로 해결할 수 있다.

1. 먼저 수열을 정렬한다. (O(N log N))
2. left 포인터는 수열의 맨 앞, right 포인터는 수열의 맨 뒤에 위치시킨다.
3. 두 포인터가 가리키는 수의 합이 13보다 작으면 left 포인터를 오른쪽으로 한 칸 이동시킨다.
4. 두 포인터가 가리키는 수의 합이 13보다 크면 right 포인터를 왼쪽으로 한 칸 이동시킨다.
5. 두 포인터가 가리키는 수의 합이 13과 같으면 경우의 수를 하나 증가시키고, left 포인터를 오른쪽으로 한 칸 이동시킨다.
6. left 포인터가 right 포인터보다 커질 때까지 3~5번 과정을 반복한다. (배열을 순회하는 비용은 O(N))

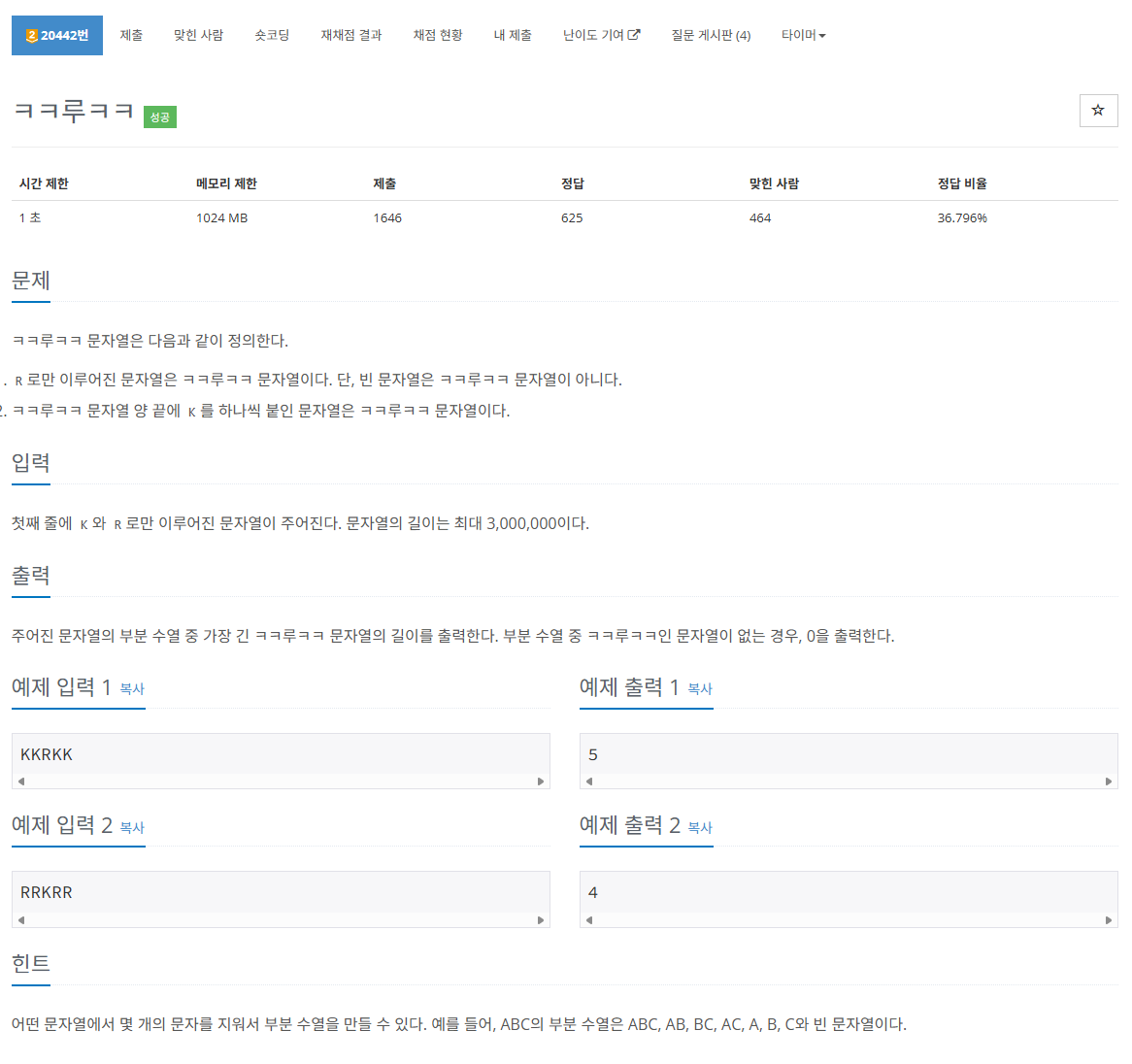
백준 20442번 ㅋㅋ루ㅋㅋ

---

https://www.acmicpc.net/problem/20442

이 문제는 어려웠다..

우선 입력 문자열의 길이가 300만이기에 O(N^2) 알고리즘은 불가능하다.

ㅋㅋ루ㅋㅋ 문자열은 좌우대칭인데, 양 끝에 K가 존재하거나 없을 수도 있고, 그 사이에 있는 R의 개수가 최대가 되어야 한다.

주어진 입력 문자열의 부분 수열 중에 가장 긴 ㅋㅋ루ㅋㅋ 문자열의 길이를 구하는 문제이다.

1. 우선 입력 문자열에서 K와 R의 개수를 미리 세어둔다.
2. 두 포인터와 정답이 될 최대 길이를 설정한다. (left = -1, right = s.length(), answer = 0)
3. 여기서부터가 중요한데, K가 양 끝에 i개 있다고 생각하며 반복문을 순회한다.
   • 입력 문자열에서 K가 8개 있었다면 K가 양 끝에 0개, 1개, 2개, …, 4개 있을 수 있기에, i는 0부터 K의 개수의 절반까지 순회한다. (i < num_k / 2 + 1)
   • left와 right는 R의 개수를 조절하기 위한 포인터이다. 현재 해당 포인터가 가리키는 문자가 R이라면 이 R을 부분 수열에서 제외시키는 역할이다.
   • left와 right가 R의 개수를 줄였다면, 다음 반복문을 돌면서 제거된 R을 제외하고 K가 양 끝에 i개 있다고 가정했을 때의 ㅋㅋ루ㅋㅋ 문자열의 길이를 계산한다.

#include <iostream>
#include <queue>
#include <algorithm>

int main()
{
    std::ios_base::sync_with_stdio(false);
    std::cin.tie(nullptr);
    std::cout.tie(nullptr);
    
    std::string s;
    std::cin >> s;
    
    int num_k = 0, num_r = 0;
    
    for (const auto& elem : s)
    {
        if (elem == 'K')
        {
            num_k++;
        }
        if (elem == 'R')
        {
            num_r++;
        }
    }
    
    int left = -1;
    int right = s.length();
    int answer = 0;
    
    for (int i = 0; i < num_k / 2 + 1 ; i++)
    {
        if (num_r == 0) break;
        
        answer = std::max(answer, 2 * i + num_r);
        
        left += 1;
        right -= 1;
        
        while (left < right && s[left] != 'K')
        {
            left += 1;
            num_r -= 1;
        }
        while (left < right && s[right] != 'K')
        {
            right -= 1;
            num_r -= 1;
        }
    }
    
    std::cout << answer;
    
    return 0;
}

참고

• https://blog.system32.kr/359