스위핑 Sweeping

Posted Dec 10, 2025

By JJM

views 5 min read

스위핑 Sweeping

이 글은 제 개인적인 공부를 위해 작성한 글입니다.
틀린 내용이 있을 수 있고, 피드백은 환영합니다.

개요

스위핑(Sweeping)은 ‘쓸다’, ‘훑어보다’라는 의미 그대로, 공간이나 직선 상에서 한쪽 끝부터 다른 쪽 끝까지 가상의 선을 이동시키면서 문제를 해결해 나가는 방식이다

가상의 선이 이동하면서 특정 요소와 마주칠 때마다 그 요소에 대해 정의된 연산을 수행하며 최종 답을 구한다.

이러한 기법을 사용하면 일반적으로 좌표의 범위가 매우 클 때, 모든 좌표를 배열 등으로 저장할 필요 없이 효율적으로 문제를 해결할 수 있다.

백준 2170번 : 선 긋기

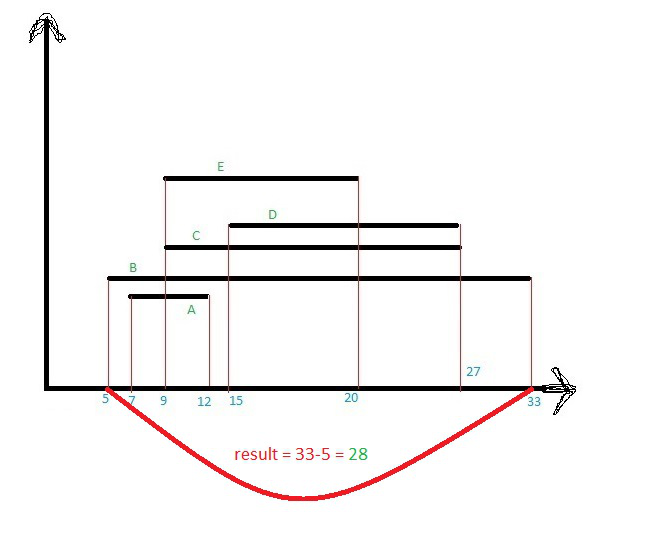
이 문제는 여러 개의 선분이 주어졌을 때, 이 선분들을 모두 덮는 데 필요한 선분의 총 길이를 구하는 문제이다.

주어진 선분들이 서로 겹칠 수 있기에, 겹치는 부분을 한 번만 세어 최종적으로 합쳐진 선분들의 총 길이를 계산해야 한다.

이 문제에서 처리해야 할 특정 요소는 각 선분의 시작점과 끝점이다.

먼저 모든 선분 N개를 시작점을 기준으로 오름차순으로 정렬한다. 만약 시작점이 같다면 끝점을 기준으로 오름차순으로 정렬한다.

이제 정렬된 선분들을 순서대로 하나씩 훑어 나간다. 또한 현재까지 처리한 선분들을 모두 덮은 하나의 큰 선분을 관리한다. 이 선분의 시작점을 Start, 끝점을 End라고 하자.

첫 번째 선분의 시작점과 끝점을 Start와 End로 초기화한다.
다음 선분부터는 두 가지 케이스가 있다.
- 현재 선분의 시작점이 End보다 작거나 같다면, 즉 겹치는 부분이 있다면, End를 현재 선분의 끝점과 비교하여 더 큰 값으로 갱신한다.
- 현재 선분의 시작점이 End보다 크다면, 즉 겹치지 않는다면, 지금까지의 Start와 End를 이용해 선분의 길이를 계산하여 총 길이에 더하고, Start와 End를 현재 선분의 시작점과 끝점으로 갱신한다.
모든 선분을 처리한 후에는 마지막으로 남아있는 Start와 End를 이용해 선분의 길이를 계산하여 총 길이에 더한다.

시간 복잡도는 $O(N \log N)$으로 N은 선분의 개수이고, log N은 정렬에 소요되는 시간이다. 선분을 순회하는 데는 O(N)의 시간이 걸린다.

  
#include <algorithm>
#include <iostream>
#include <vector>

struct Line
{
    int s;
    int e;

    Line(int inX, int inY) : s(inX), e(inY) {}

    bool operator<(const Line& other) const
    {
        if (s != other.s)
        {
            return s < other.s;
        }
        return e < other.e;
    }
};

int main()
{
    std::ios_base::sync_with_stdio(false);
    std::cin.tie(nullptr);
    std::cout.tie(nullptr);

    std::vector<Line> lines;
    int n;
    std::cin >> n;

    int x, y;
    for (int i = 0; i < n; i++)
    {
        std::cin >> x >> y;
        lines.emplace_back(x, y);
    }

    std::sort(lines.begin(), lines.end());

    int answer = 0;
    int start = lines[0].s;
    int end = lines[0].e;
    
    for (int i = 1; i < n; i++)
    {
        if (end >= lines[i].s)
        {
            end = std::max(end, lines[i].e);
        }
        else if (end < lines[i].s)
        {
            answer += end - start;
            start = lines[i].s;
            end = lines[i].e;
        }
    }

    answer += end - start;

    std::cout << answer;

    return 0;
}

참고

Algorithm

This post is licensed under CC BY 4.0 by the author.

개요

백준 2170번 : 선 긋기

Trending Tags