[운영체제 아주 쉬운 세 가지 이야기 - Virtualization] 20. Advanced Page Tables

Posted Aug 19, 2025

Operating System

By JJM

views 41 min read

이 글은 제 개인적인 공부를 위해 작성한 글입니다.
틀린 내용이 있을 수 있고, 피드백은 환영합니다.

개요

페이징의 두 번째 문제점은 페이지 테이블의 크기이다. 페이지 테이블이 크면 많은 메모리 공간을 차지한다. 배열 형태를 가지는 선형 페이지 테이블을 살펴보자.

페이지 크기가 4KB, 2^12바이트이고, 페이지 테이블의 각 항목은 4바이트인 32비트 주소 공간, 2^32바이트를 가정해 보자. 주소 공간에는 대략 백만 개 (2^32 / 2^12)의 가상 페이지가 존재할 것이다. 여기에 페이지 테이블 항목의 크기를 곱하면 하나의 페이지 테이블 크기는 약 4MB가 된다.

그리고 일반적으로 각 프로세스는 자기 자신의 페이지 테이블을 갖기에 프로세스가 백 개라면 400MB의 메모리가 필요하다. 이런 엄청난 메모리 부담을 어떻게 해결할 수 있을까.

단순 배열 기반의 페이지 테이블은 크기가 크며 일반적인 시스템에서 메모리를 과도하게 차지한다. 어떻게 페이지 테이블의 크기를 줄일 수 있으며 주요 개념들로는 무엇이 있을까? 새로운 자료구조들은 어떤 비효율성을 가질까?

간단한 해법 : 더 큰 페이지

페이지 테이블의 크기를 간단하게 줄일 수 있는 한가지 방법은 페이지 크기를 증가시키는 것이다. 32비트 주소 공간에서, 16KB 페이지 크기를 사용한다면 18비트의 VPN과 14비트의 오프셋을 가지게 된다. 각 PTE(4바이트)의 크기가 모두 동일하다면, 페이지 테이블에 2^18개의 항목이 있으며, 페이지 테이블의 총 크기는 1MB가 된다. 페이지 크기가 4배 증가했기에 페이지 테이블의 크기는 1/4로 감소한다.

페이지 크기 증가의 가장 큰 문제는 내부 단편화(internal fragmentation)이다. 페이지 내부의 낭비되는 공간이 많아진다.

응용 프로그램이 여러 페이지를 할당받았지만, 할당 받은 페이지의 일부분만 사용하는 터에, 컴퓨터 시스템의 메모리가 금방 고갈된다. 이런 이유에서 많은 컴퓨터 시스템들이 4KB나 8KB 같이 비교적 작은 페이지들을 사용한다.

하이브리드 접근 방법 : 페이징과 세그먼트

1KB 크기의 페이지를 갖는 16KB의 주소 공간을 예시로 알아보자. 16KB의 아주 작은 주소 공간에서 페이지 테이블 대부분이 비어있는 엄청난 낭비가 발생했다.

결합 방식을 생각해 보자. 프로세스의 전체 주소 공간을 위해 하나의 페이지 테이블을 두는 대신, 논리 세그멘트마다 따로 페이지 테이블을 두면 어떨까? 이 예제에서는 코드, 힙, 스택 세그먼트에 대해 3개의 페이지 테이블이 있을 수 있다.

세그멘테이션에서는 세그멘트의 물리 주소 시작 위치를 나타내는 베이스 레지스터, 그리고 크기를 나타내는 바운드 또는 리미트 레지스터가 있다. 우리의 결합 방식에서도 MMU에 비슷한 구조를 사용한다.

베이스 레지스터는 세그멘트 시작 주소를 가리키는 것이 아니라 세그멘트의 페이지 테이블의 시작 주소를 갖는다. 바운드 레지스터는 페이지 테이블의 끝을 나타내기 위해서 사용한다.

간단한 예를 들어보자. 4KB 페이지를 갖는 32비트 가상 주소 공간이 4개의 세그먼트로 나뉘어져 있고 코드, 힙, 스택 세 개의 세그먼트만 사용해보자.

소속 세그멘트를 나타내기 위해 상위 두 비트를 사용하낟. 미 사용 세그멘트는 00, 코드는 01, 힙은 10, 스택은 11을 나타낸다.

하드웨어에 세 개의 베이스/바운드 레지스터 쌍이 코드와 힙 그리고 스택을 위해서 존재한다. 실행 중인 프로세스에서, 각 세그멘트의 베이스 레지스터는 각 세그멘트 페이지 테이블의 시작 물리 주소를 갖게 된다. 이 시스템에서 모든 프로세스들은 세 개의 페이지 테이블을 갖는다. 문맥 교환 시, 이 레지스터들은 새로 실행되는 프로세스의 페이지 테이블의 위치값으로 변경된다.

TLB 미스가 발생(하드웨어 기반 TLB로 가정)하면 하드웨어는 세그멘트 비트(SN)을 사용하여 어떤 베이스와 바운드 쌍을 사용할지 결정한다. 하드웨어는 그 레지스터에 들어 있는 물리 주소를 VPN과 다음과 같은 형식으로 조작하여 PTE의 주소를 얻는다.

앞에서 살펴보았던 선형 페이지 테이블의 작동과 거의 동일하고, 유일한 차이는 하나의 페이지 테이블 베이스 레지스터를 사용하는 대신 세 개 중의 하나의 세그멘트 베이스 레지스터를 사용하는 것이다.

하이브리드 기법에서 핵심은 세그멘트마다 바운드 레지스터가 따로 존재한다는 것이다. 각 바운드 레지스터의 값은 세그멘트의 최대 유효 페이지의 개수를 나타낸다.

예를 들어, 첫 세 개의 페이지들(0, 1, 2)을 코드 세그멘트로서 사용 중이라면, 코드 세그멘트 페이지 테이블은 세 개의 항목만 할당을 받을 수 있을 것이고 바운드 레지스터는 3으로 설정된다. 해당 세그멘트의 범위가 넘어가는 곳에 대한 메모리 접근은 예외를 발생시키고, 해당 프로세스는 종료될 것이다.

이와 같은 방식으로, 하이브리드 기법은 선형 페이지 테이블에 비해 메모리 사용을 개선시킬 수 있다. 스택과 힙 사이의 할당되지 않은 페이지들은 페이지 테이블 상에서 더 이상 공간을 차지하지 않는다.

하지만 여전히 세그멘테이션을 사용해야 하기에 단점이 있다. 세그멘테이션은 주소 공간의 사용에 있어 특정 패턴을 가정하기 때문에 우리가 원하는 만큼은 유연하지가 못하다. 큰 공간을 커버하지만, 드문드문 사용되는 힙의 경우 여전히 페이지 테이블의 낭비를 면치 못할 수가 있다. 또한 하이브리드 기법은 외부 단편화를 유발한다. 페이지 테이블 크기에 제한이 없으며 다양한 크기를 갖고, 페이지 테이블의 크기는 페이지 테이블 항목 크기의 정수배가 되어야 한다. 메모리 상에서 페이지 테이블용 공간을 확보하는 것이 더 복잡하다.

멀티 레벨 페이지 테이블

세그멘테이션을 사용하지 않고 페이지 테이블 크기를 줄이는 방법에 대해서 생각해 보자. 어떻게 하면 사용하지 않는 주소 공간을 페이지 테이블에서 제거할 수 있을까?

멀티 레벨 페이지 테이블(MLPT)에서는 선형 페이지 테이블을 트리 구조로 표현한다. 매우 효율적이기 때문에 많은 현대 시스템에서 사용되고 있다.

MLPT의 기본 개념은 간단하다. 먼저, 페이지 테이블을 페이지 크기의 단위로 나눈다. 그 다음, 페이지 테이블의 페이지가 유효하지 않은 항목만 있으면, 해당 페이지를 할당하지 않는다. 페이지 디렉터리(page directory)라는 자료 구조를 사용하여 페이지 테이블 각 페이지의 할당 여부와 위치를 파악한다. 페이지 디렉터리는 페이지 테이블을 구성하는 각 페이지의 존재 여부와 위치 정보를 가지고 있다.

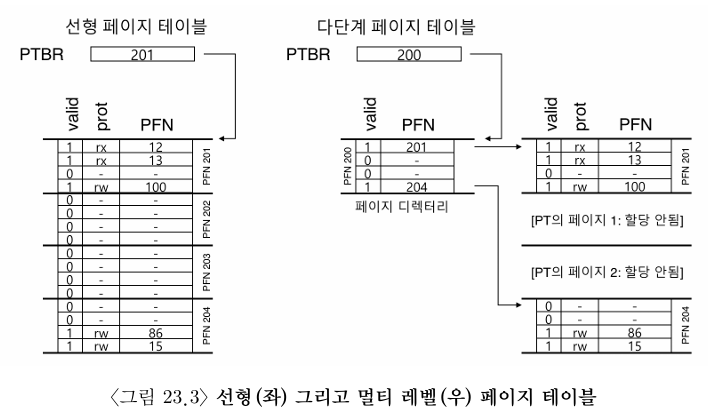
위 예제를 살펴보자. 좌측 그림은 전형적인 선형 페이지 테이블이다. 페이지 테이블의 중앙부에 해당하는 주소 공간은 사용되고 있지 않다. 그러나 페이지 테이블에서 항목들이 할당되어 있다.

우측은 동일한 주소 공간을 다루는 MLPT이다. 페이지 디렉터리에는 두 개의 유효한 페이지가 있고, 메모리에 존재한다.

이 예를 통해 MLPT에서는 선형 페이지 테이블에서 사용되었던 페이지들이 더 이상 필요없고, 페이지 디렉터리를 이용하여 페이지 테이블의 어떤 페이지들이 할당되었는지를 관리한다는걸 알 수 있다.

간단한 2단계 테이블에서 페이지 디렉터리의 각 항목은 페이지 테이블의 한 페이지를 나타낸다. 페이지 디렉터리는 페이지 디렉터리 항목(page directory entries, PDE)들로 구성된다. 각 PDE의 구성은 페이지 테이블의 각 항목(PTE)과 유사하다. 유효 비트와 페이지 프레임 번호(PFN)를 갖고 있다.

하지만 PTE의 유효 비트와 PDE의 유효 비트는 약간 다르다. PDE 항목이 유효하다는 것은, 그 항목이 가리키고 있는 페이지들 중 최소한 하나가 유효하다는 것을 의미한다. 즉, PDE가 가리키고 있는 페이지 내의 최소한 하나의 PTE의 유효 비트가 1로 설정되어 있다. PDE 항목이 유효하지 않다면 PDE는 실제 페이지가 할당되어 있지 않은 것이다.

MLPT는 다른 기법들에 비해 몇 가지 장점이 있다.

멀티 레벨 테이블은 사용된 주소 공간의 크기에 비례하여 페이지 테이블 공간이 할당된다.

그렇기 때문에, 보다 작은 크기의 페이지 테이블로 주소 공간을 표현할 수 있다.

페이지 테이블을 페이지 크기로 분할함으로써 메모리 관리가 매우 용이하다.

페이지 테이블을 할당하거나 확장할 때, 운영체제는 가용 페이지 풀에 있는 빈 페이지를 가져다 쓰면 된다. 멀티 레벨 페이징을 단순한 선형 페이지 테이블 방식과 비교해 보자. 선형 페이지 테이블의 각 항목은 해당 가상 페이지의 물리 페이지 주소를 가지고 있고, (즉, 디스크로 스왑되지 않는다) 연속된 물리 메모리 공간을 차지한다.

4MB의 큰 페이지 테이블의 경우, 해당 크기의 연속된 빈 물리 메모리를 찾는 것이 쉽지 않다. 멀티 레벨 페이징에서는 페이지 디렉터리를 사용하여 각 페이지 테이블 페이지들의 위치를 파악한다. 페이지 테이블의 각 페이지들이 물리 메모리애 퍼져있더라도 페이지 테이블 디렉터리를 이용하여 그 위치를 파악할 수 있으므로, 페이지 테이블을 위한 공간 할당이 매우 유연하다.

시간과 공간 간의 절충점에 대해 이해하자
자료 구조 설계 시, 구현에서 시간과 공간의 소요 시간을 적절히 절충(trade-off)해야 한다. 일반적으로 자료 구조에 접근 속도를 향상시키려면, 해당 구조를 위해 공간을 더 사용해야 한다.

한 가지 유의해야 할 사항은, MLPT에는 추가 비용이 발생한다. TLB 미스 시, 주소 변환을 위해 페이지 디렉터리와 PTE 접근을 위해 두 번의 메모리 로드가 발생한다. 선형 페이지 테이블에서는 한 번의 접근만으로 주소 정보를 TLB로 탑재한다.

MLPT은 시간(페이지 테이블 접근 시간)과 공간(페이지 테이블 공간)의 살호 절충(time-space-trade-off)의 한 예라 할 수 있다. 페이지 테이블 크기를 줄이는 데 성공하였으나, 메모리 접근 시간이 증가했다. TLB 히트 시 성능은 동일하지만, TLB 미스 시에는 두 배의 시간이 소요된다.

또 하나의 단점은 복잡도이다. 페이지 테이블 검색이 단순 선형 페이지 테이블의 경우보다 더 복잡해진다. 검색을 하드웨어/운영체제 어떤 것으로 구현하느냐 여부와는 무관하다. 대부분의 경우, 성능 개선이나 부하 경감을 위해, 우리는 보다 복잡한 기법을 도입한다. MLPT의 경우에는 메모리 자원의 절약을 위해 페이지 테이블 검색을 더 복잡하게 만들었다.

멀티 레벨 페이징 예제

MLPT의 개념을 이해하기 위해 예제를 하나 살펴보자. 64바이트 페이지를 갖는 16KB 크기의 작은 주소 공간을 생각해보자. 14비트 가상 주소 공간이다.

VPN에 8비트, 페이지 오프셋에 6비트가 필요하다. 선형 페이지 테이블은 2^8(256)개의 엔트리로 구성된다. 주소 공간에는 작은 부분만 사용된다 하더라도, 선형 페이지 테이블의 크기는 변하지 않는다.

가상 페이지 0과 1은 코드, 4와 5는 힙, 254와 255는 스택으로 사용된다. 주소 공간의 나머지 페이지들은 미사용 중이다.

이 주소 공간을 2단계 페이지 테이블로 구성해 보자. 선형 페이지 테이블을 페이지 단위로 분할한다. 전체 테이블은 256개의 항목을 가지고, 각 PTE는 4바이트라 가정하자. 페이지 테이블의 크기는 1KB(256 * 4바이트)이다. 페이지가 64바이트라고 하면 1KB의 페이지 테이블은 16개의 64바이트 페이지들로 분할된다. 각 페이지에는 16개의 PTE가 있다.

이제 VPN으로부터 페이지 디렉터리 인덱스를 추출하고, 페이지 테이블의 각 페이지 위치를 파악하는 법을 살펴보자. 페이지 디렉터리, 페이지 테이블의 페이지들 모두 항목의 배열이라는 것을 기억해야 한다. VPN을 이용하여 인덱스를 구성하는 법만 찾으면 된다.

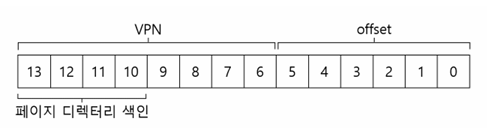
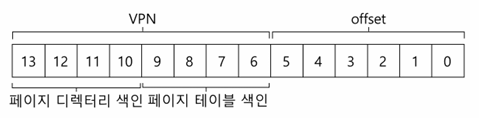
먼저 페이지 디렉터리와 인덱스를 만들어보자. 예제의 작은 페이지 테이블은 256개의 항목으로 16개의 페이지로 나뉘어 있다. 페이지 디렉터리는 페이지 테이블의 각 페이지마다 하나씩 있어야하기 때문에 총 16개의 항목이 있어야 한다. 결과적으로 VPN의 4개의 비트를 사용하여 디렉터리를 구성하며, 여기서는 VPN의 상위 4비트를 다음과 같이 사용한다.

VPN에서 페이지-디렉터리 인덱스(page-directory index, PDIndex)를 추출하고 나면

PDEAddr = PageDirBase + (PDIndex * sideof(PDE))라는 간단한 식을 사용하여 PDE의 주소를 찾을 수 있다.

페이지 디렉터리의 해당 항목이 무효라고 표시되어 있으면, 이 주소 접근은 유효하지 않기에, 예외가 발생한다. 해당 PDE가 유효하다면 추가 작업을 해야 한다.

이 페이지 디렉터리 항목이 가리키고 있는 페이지 테이블의 페이지에서 원하는 PTE을 읽어 들이는 것이 목표다. 이 PTE를 찾기 위해 VPN의 나머지 비트들을 사용한다.

이 페이지-테이블 인덱스(page-table index, PTIndex)는 페이지 테이블 자체 인덱스로 사용된다. PTE의 주소를 다음과 같이 계산한다.

PTEAddr = (PDE.PFN « SHIFT) + (PTIndex * sizeof(PTE))

PTE의 주소를 생성하기 위해서는 PDE에서 얻은 PFN을 좌측 쉬프트 연산하고 그 값을 PTIndex에 합산한다.

2단계 이상 사용하기

지금까지는 멀티 레벨 페이지 테이블은 페이지 디럭테리와 페이지 테이블의 2개 단계를 가정하였다. 경우에 따라서 트리의 단계를 더 증가시키는 것도 가능하고, 그래야 한다.

이 예제에서는 512바이트 페이지와 30비트 가상 주소 공간을 가정한다. 가상 주소는 21비트의 가상 페이지 번호와 9비트의 오프셋을 갖게 된다.

MLPT의 목적은 페이지 테이블의 모든 분할된 부분들이 단일 페이지 크기에 맞도록 하는 것이다. 만약 페이지 디렉터리가 너무 커지면 어떻게 될까?

멀티 레벨 테이블에서 몇 단계를 둘지 정하기 위해서는 먼저 한 페이지에 몇 개의 페이지 테이블 항목을 저장할 수 있을지를 계산해야 한다. 페이지 크기가 512바이트이고 PTE의 크기가 4바이트라고 가정하면 한 페이지에 128개의 PTE를 넣을 수 있다. 페이지 테이블의 페이지를 인덱스로 쓰려면, VPN의 하위 7비트(log2(128))가 필요하다.

페이지 디렉터리를 위해서 몇 개의 비트가 남았는지를 이 그림에서 알 수 있다. 14개의 비트가 남는다. 2단계 페이지를 사용한다면 페이지 디렉터리에 2^14개의 항목이 있게 된다. 페이지 디렉터리를 위해서 128 페이지 분량의 연속된 메모리가 필요하다. 페이지 테이블을 페이지 단위로 나누어 배치할 수 있도록 하는 멀티 레벨 페이지 테이블의 근본 취지가 훼손된 셈이다.

이 문제를 해결하기 위해서, 페이지 디렉터리 자체를 멀티 페이지들로 나누어서 트리의 단계를 늘리도록 한다. 그리고 페이지 디렉터리의 페이지들을 가리킬 수 있도록 그 위에 새로운 페이지 디렉터리를 추가한다. 결과적으로 위와 같이 가상 주소를 분할할 수 있다.

이제 가상 주소의 최상위 비트들을(PD Index 0) 사용하여 상위 단계의 페이지 디렉터리에서 엔트리를 찾는다. 이 인덱스를 사용하여 상위 단계 페이지 디렉터리에서 PDE를 가져온다. 만약 유효하다면, 상위 단계 페이지 디렉터리에서 얻은 물리 주소와 두 번째 단계의 PDIndex 1 를 결합하여 페이지 테이블 인덱스가 존재한 물리 페이지를 구한다. 해당 페이지가 유효할 경우, 최종적으로, PTE 주소는 2번째 단계의 페이지 디렉터리 항목에서 얻은 페이지 테이블의 물리 주소와 페이지 테이블 인덱스를 결합하여 구한다. 실제 주소를 구하는데 드는 작업이 상당한데, MLPT 사용 시 수반되는 작업이다.

변환 과정 : TLB를 기억하자

2단계 페이지 테이블 시, 전체 주소 변환 과정을 알고리즘 형태로 요약 정리해 보자. 이 그림은 모든 메모리 참조에 대해 하드웨어가 어떤 식으로 동작하는지를 나타낸다.

MLPT 접근을 거치기 전에 우선 TLB를 검사한다.
하트라면 페이지 테이블 참조 없이 물리 주소를 직접 구성한다.
미스라면 MLPT의 모든 단계를 거쳐 물리 주소를 구하게 된다.

이 알고리즘을 통해 TLB 미스 시, 전통적인 2단계 페이지 테이블의 주소 계산 비용을 볼 수 있다. 주소 변환을 위해 두 번의 추가 메모리 접근이 발생한다.

역 페이지 테이블

좀 더 획기적인 공간 절약 방법으로 역 페이지 테이블(inverted page table)이 있다. 이 방법에서는 여러 개의 페이지 테이블(시스템의 프로세스 당 하나씩) 대신 시스템에 단 하나의 페이지 테이블만 둔다. 페이지 테이블은 물리 페이지를 가상 주소 상의 페이지로 변환한다. 역 페이지 테이블의 각 항목은 해당 물리페이지를 사용 중인 프로세스 번호, 해당 가상 페이지 번호를 갖고 있다.

페이지 테이블의 목적은 가상 주소를 물리 주소로 변환하는 것이지만, 역 페이지 테이블에서는 주소 변환을 위해 전체 테이블을 검색해서 원하는 가상 주소 페이지를 갖는 항목을 찾아야 한다. 순차 탐색은 느리기에 주로 해시 테이블을 사용한다.

일반적인 시각에서 보면 역 페이지 테이블 역시 하나의 자료 구조일 뿐이다. MLPT와 역 페이지 테이블은 할 수 있는 다양한 방법 중 두 가지 예일 뿐이다.

페이지 테이블을 디스크로 스와핑하기

이제까지는 페이지 테이블이 커널이 소유하고 있는 물리 메모리 영역에 존재한다고 가정하였다. 페이지 테이블 크기 축소를 위해 많은 시도를 하더라도, 여전히 모든 페이지 테이블을 메모리에 상주시키기에는 양이 너무 클 수도 있다. 그렇기 떄문에 어떤 시스템들은 페이지 테이블들을 커널 가상 메모리에 존재시키고, 시스템의 메모리가 부족할 경우, 페이지 테이블을 디스크로 스왑(swap)하기도 한다. 이 부분에 대해서는 나중에 다뤄보자.

요약

1. 더 큰 페이지 : Huge Pages

페이지 크기를 키워 전체 페이지 수를 줄임으로써 페이지 테이블의 크기를 줄이는 가장 간단한 방법

TLB의 Hit를 높여주는, 반대로 TLB의 Miss를 줄여주는 효과가 있다.

TLB 히트를 높여 캐시 사용률을 높여주면 데이터 접근이 빨라진다.

하지만 할당된 페이지 내에서 사용되지 않는 공간이 늘어나는 내부 단편화 문제가 발생할 수 있다.

2. 페이징과 세그멘테이션 하이브리드 기법

코드, 힙, 스택과 같은 논리적 세그멘트마다 별도의 페이지 테이블을 두는 방식

힙과 스택 사이의 거대한 미사용 공간에 대한 페이지 테이블 항목을 생성하지 않아 메모리를 절약할 수 있다.

하지만 외부 단편화 문제가 발생할 수 있고, 세그멘테이션 고유의 유연성 부족이라는 단점을 가진다.

3. 멀티 레벨 페이지 테이블

페이지 테이블을 다시 페이지 크기로 나누고, 페이지 디렉터리라는 상위 자료 구조를 통해 트리 형태로 관리하는 방식

사용되는 주소 공간에 비례하여 페이지 테이블 공간을 할당하므로 메모리 효율이 높다.

하지만 TLB 미스가 발생하면 주소 변환을 위해 여러 번 메모리에 접근해야 하므로 성능 저하의 원인이 될 수 있다.

4. 역 페이지 테이블

프로세스마다 페이지 테이블을 두는 대신, 시스템 전체에 물리 페이지 프레임에 대응하는 단 하나의 테이블을 두는 방식

테이블 크기가 가상 주소 공간이 아닌 물리 메모리 크기에 비례하므로 공간을 크게 절약할 수 있다

하지만 주소 변환을 위해 테이블을 검색해야 하므로 (주로 해시 테이블) 구현이 복잡하다.

4 Level Page Table

선형 페이지 테이블을 32비트 시스템에서 4KB 페이지 크기를 사용한다고 가정하면,

가상 주소 공간 : 2^32 = 4GB
페이지 크기 : 4KB = 2^12
필요한 페이지 수 : 2^32 / 2^12 = 2^20 = 약 백만개
페이지 테이블 엔트리 크기 : 4바이트
페이지 테이블 크기 : 약 백만 * 4바이트 = 약 4MB

백 개의 프로세스가 실행 중이라면 400MB의 메모리가 필요하다.

64비트 시스템에서는 더 심각하다.

가상 주소 공간 : 2^64 (실제로는 48비트 정도 사용)
필요한 페이지 수 : 2^48 / 2^12 = 2^36 = 약 687억개
페이지 테이블 크기 : 약 687억 * 4바이트 = 약 274GB

이는 물리적으로 불가능한 크기이다.

4단계 페이지 테이블은 현대 64비트 시스템에서 사용되고, 대표적으로 x86-64 아키텍처에서 사용된다.

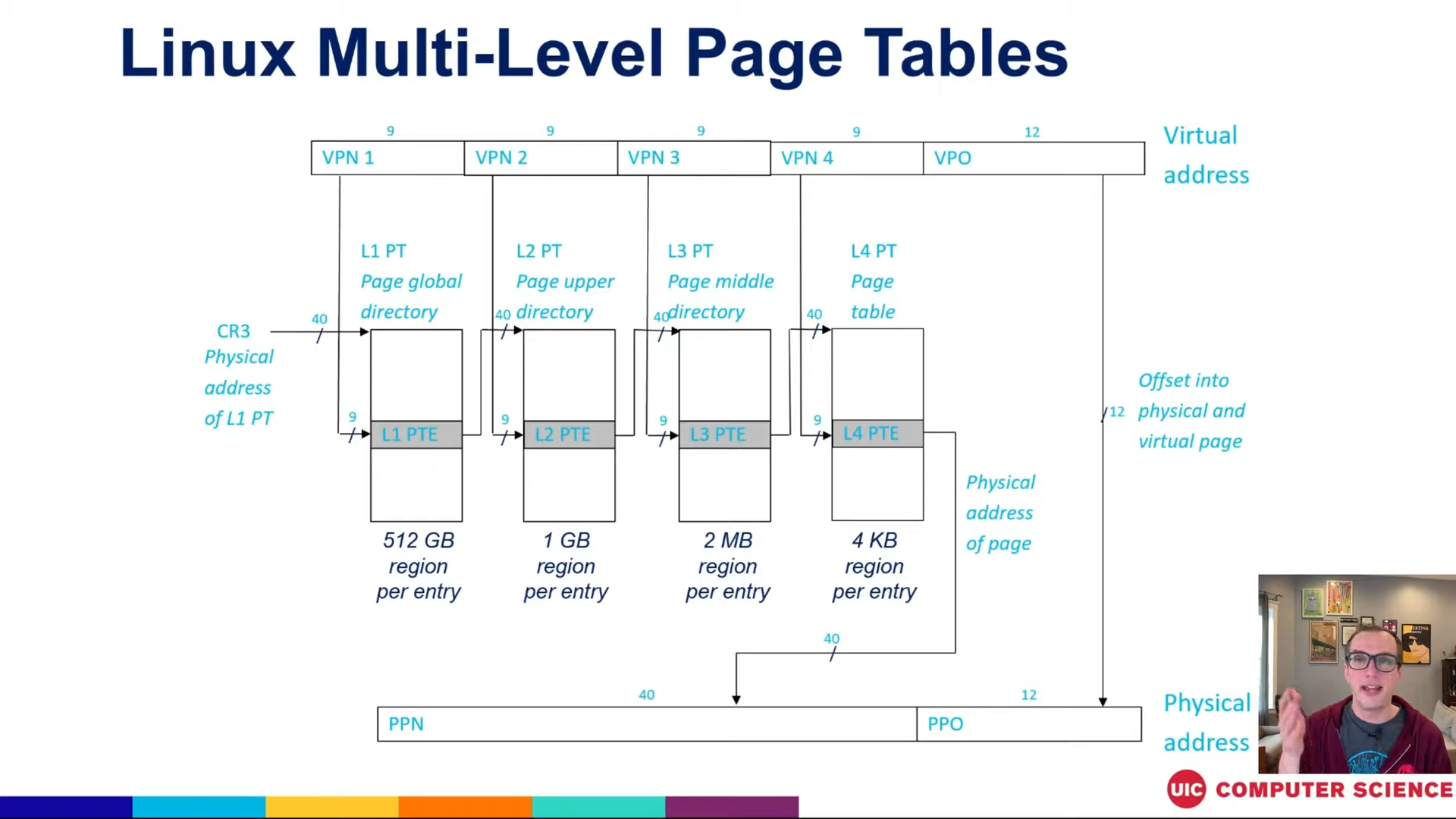
x86-64 아키텍처에서는 9비트 (PML4) + 9 bit (PDPT) + 9 bit (PDT) + 9 bit (PTE) + 12 bit (Offset) = 총 48비트의 가상 주소를 사용한다.

PML4 : Page Map Level 4, 최상위 페이지 테이블.
PDPT : Page Directory Pointer Table, PML4의 각 항목이 가리키는 테이블.
PDT : Page Directory Table, PDPT의 각 항목이 가리키는 테이블.
PT : Page Table, PDT의 각 항목이 가리키는 가장 하위 레벨의 테이블.

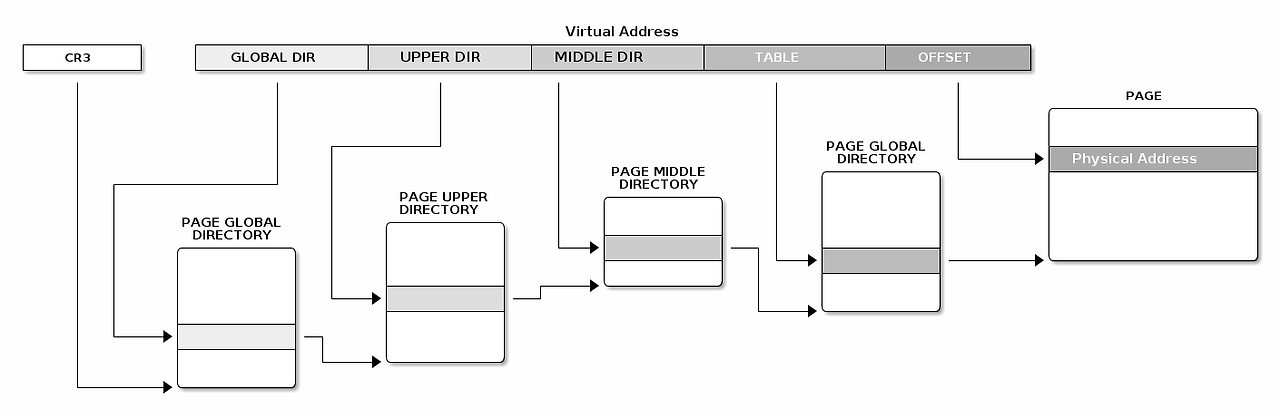
linux 커널에서는 9 bit (PGD) + 9 bit (PUD) + 9 bit (PMD) + 9 bit (PTE) + 12 bit (Offset) = 총 48비트의 가상 주소를 사용한다.

PGD : Page Global Directory
PUD : Page Upper Directory
PMD : Page Middle Directory
PTE : Page Table Entry

개념적으로 동일하지만, 용어가 다르다고 이해하였다.

CPU에서 특정 가상 주소에 접근하려고 할 때, 다음과 같은 단계를 거쳐 물리 주소를 찾아낸다.

CR3(Control Register)라는 레지스터가 최상위 테이블인 PML4의 물리 주소 시작점을 저장하고 있다.

PML4 조회
- CR3 레지스터가 가리키는 PML4 테이블의 시작 주소를 찾는다.
- 가상 주소의 PML4 인덱스를 사용하여 PML4 테이블 내에서 해당 엔트리를 찾는다.
- 이 엔트리에는 아래 단계인 PDPT의 물리적 시작 주소가 들어있다.
PDPT 조회
- 1단계에서 찾은 주소를 기반으로 PDPT에 접근한다.
- 가상 주소의 PDPT 인덱스를 사용하여 PDPT 테이블 내에서 해당 엔트리를 찾는다.
- 이 엔트리에는 아래 단계인 PDT의 물리적 시작 주소가 들어있다.
PDT 조회
- 2단계에서 찾은 주소를 기반으로 PDT에 접근한다.
- 가상 주소의 PDT 인덱스를 사용하여 PDT 테이블 내에서 해당 엔트리를 찾는다.
- 이 엔트리에는 마지막 단계인 PT의 물리적 시작 주소가 들어있다.
PT 조회
- 3단계에서 찾은 주소를 기반으로 PT에 접근한다.
- 가상 주소의 PT 인덱스를 사용하여 PT 테이블 내에서 해당 엔트리를 찾는다.
- 이 엔트리에는 물리 페이지 프레임의 시작 주소가 들어있다.
물리 주소 계산
- 4단계에서 얻은 물리 페이지 프레임의 시작 주소와 아상 주소의 오프셋을 더해 최종 물리 주소를 계산한다.

만약 TLB 미스가 난다면, 4단계 테이블에서는 4번의 메모리 접근이 필요하다.

참고

Computer Science, Operating System