위상 정렬 Topological Sorting

본 글은 제 개인적인 공부를 위해 작성한 글입니다. 틀린 내용이 있다면 언제든지 피드백을 주시면 감사하겠습니다. 참고로만 활용해주시길 바랍니다.

개요

---

위상 정렬은 방향 그래프의 모든 노드를 주어진 방향성에 어긋나지 않게 순서대로 나열하는 알고리즘이다. 선수 과목이 있는 커리큘럼이나 조립 순서가 정해진 프라모델을 떠올리면 이해하기 쉽다. 특정 작업을 하기 전에 반드시 완료해야 하는 작업이 있을 때, 그 순서를 결정해주는 알고리즘이다.

위상 정렬은 사이클이 없는 유향 그래프(DAG, Directed Acyclic Graph)에서만 가능하다. 사이클이 있다면 위상 정렬을 수행할 수 없다. 또한 답이 여러 개일 수 있다. 선택할 수 있는 노드가 여러 개라면 정렬 결과는 다양하게 나올 수 있다.

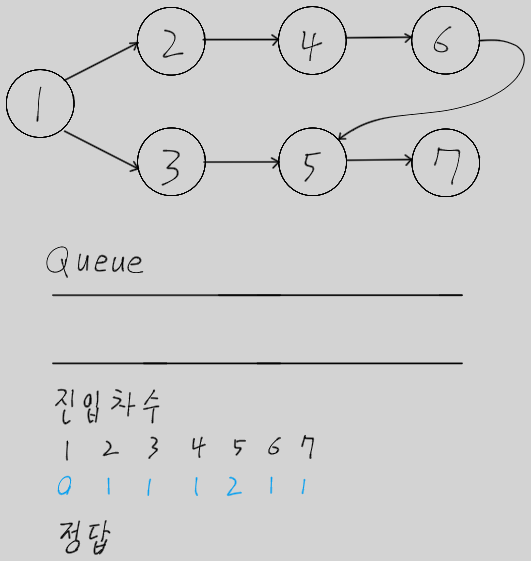
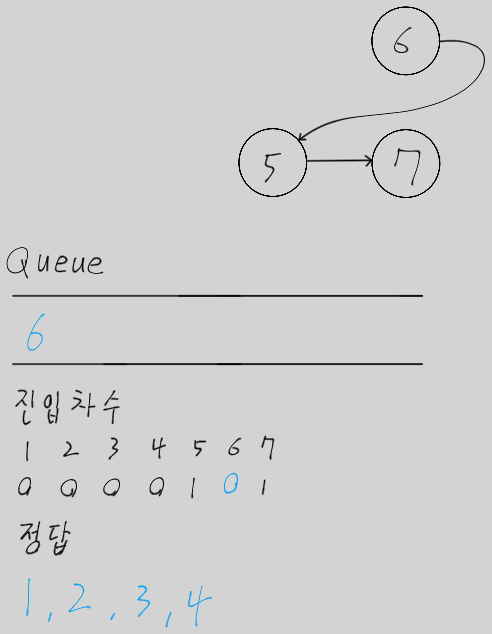
위상 정렬을 이해하려면 진입 차수(Indegree)라는 개념을 알아야 한다.

• 진입 차수 : 특정 노드로 들어오는 간선의 개수
• 진입 차수가 0인 노드 : 내 앞에 먼저 해야 할 일이 아무것도 없는 상태, 즉시 수행 가능한 작업을 의미한다.

과정

---

큐를 사용하여 구현한다.

1. 그래프의 모든 노드에 대해 진입 차수를 계산한다.
2. 진입 차수가 0인 노드를 큐에 모두 넣는다.
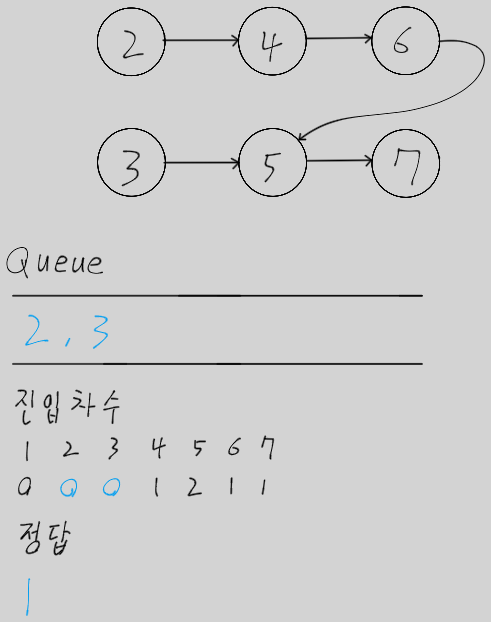
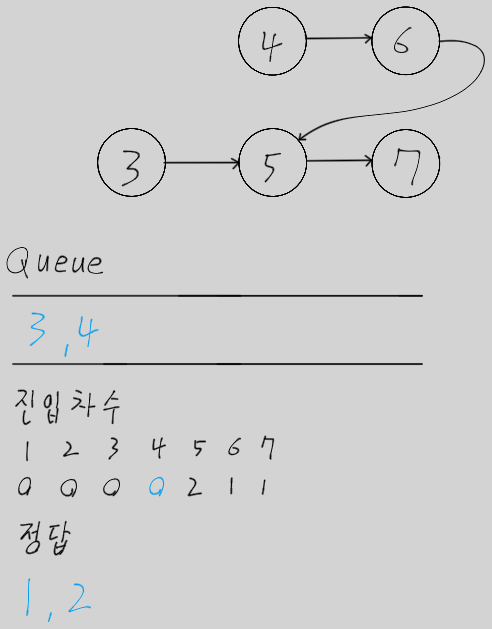
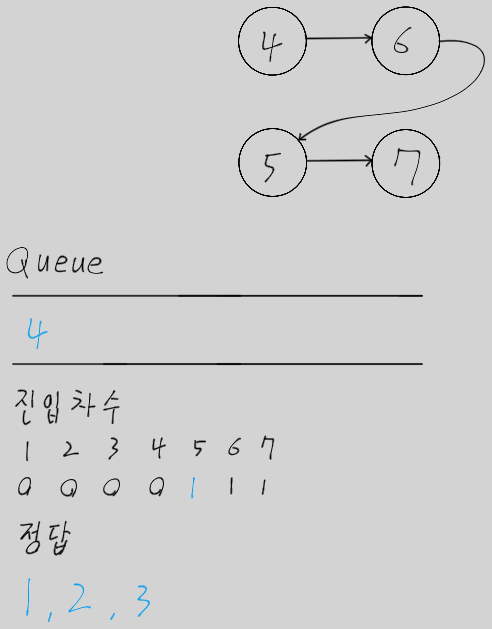
3. 큐가 빌 때까지 다음 과정을 반복한다.
   • 큐에서 노드를 꺼내 정렬 결과 리스트에 담는다.
   • 꺼낸 노드와 연결된 모든 간선을 제거한다.
   • 이로 인해 진입 차수가 0이 된 새로운 노드들을 큐에 넣는다.
4. 만약 모든 노드를 방문하기 전에 큐가 빈다면, 그래프에 사이클이 존재한다는 의미이다.
5. 모든 원소를 방문했다면 큐에서 꺼낸 순서가 위상 정렬의 결과

시간 복잡도

---

모든 노드를 확인하고, 각 노드에서 나가는 간선들을 한 번씩 모두 확인하기 때문에 $O(V+E)$이다.

백준 2623번 : 음악 프로그램

---

https://www.acmicpc.net/problem/2623

#include <iostream>
#include <queue>
#include <vector>

int main()
{
    std::ios_base::sync_with_stdio(false);
    std::cin.tie(nullptr);
    std::cout.tie(nullptr);
    
    int n, m;
    std::cin >> n >> m;
    
    std::vector graph(n + 1, std::vector<int>());
    std::vector indegree(n + 1, 0);
    
    for (int i = 0; i < m; i++)
    {
        int input_cnt;
        std::cin >> input_cnt;
        
        std::vector<int> temp(input_cnt);
        for (int j = 0; j < input_cnt; j++)
        {
            std::cin >> temp[j];
        }
        
        for (int j = 0; j < input_cnt - 1; j++)
        {
            int start = temp[j];
            int end = temp[j + 1];
            graph[start].emplace_back(end);
            indegree[end]++;
        }
    }
    
    std::queue<int> que;
    std::vector<int> answer;
    for (int i = 1; i < n + 1; i++)
    {
        if (indegree[i] == 0)
        {
            que.emplace(i);
        }
    }
    
    while (!que.empty())
    {
        int node = que.front();
        que.pop();
        answer.emplace_back(node);
        
        for (const auto& adj_node : graph[node])
        {
            if (--indegree[adj_node] == 0)
            {
                que.emplace(adj_node);
            }
        }
    }
    
    if (answer.size() == n)
    {
        for (const auto& elem : answer)
        {
            std::cout << elem << '\n';
        }
    }
    else
    {
        std::cout << 0;
    }

    return 0;
}