플로이드 워셜 Floyd Warshall

이 글은 제 개인적인 공부를 위해 작성한 글입니다.
틀린 내용이 있을 수 있고, 피드백은 환영합니다.

개요

---

• 플로이드 와샬 알고리즘은 그래프에서 모든 쌍의 최단 경로를 찾는 동적 계획법 기반의 알고리즘이다.
• 그래프의 모든 노드를 순회하며, 임의의 두 노드 i에서 j로 가는 최단 경로에 특정 노드 k를 경유했을 때, 더 짧은 노드가 생기는지 확인하고 갱신하는 방법으로 작동한다.
• $D[i][j] = min(D[i][j], D[i][k] + D[k][j])$
• $D[i][j]$ : 노드 i에서 j로 가는 최단 거리
• 음수 가중치(간선)을 허용한다. 하지만 음수 사이클이 존재하는 경우 최단 경로를 정확히 정의할 수 없으므로, 알고리즘 수행 후 D[i][j] 값이 음수인지 확인하여 음수 사이클 존재 여부를 알 수 있다.

과정

---

1. 노드 i에서 j로 가는 거리를 초기화한다.
2. 간선이 존재하면 그 간선의 가중치로, 간선이 없으면 무한대로 설정한다.
3. 자기 자신으로 가는 거리는 0으로 설정한다.
4. 경유지 k를 1부터 N까지 순서대로 선택한다.
5. 출발 노드 i를 1부터 N까지 순서대로 선택한다.
6. 도착 노드 j를 1부터 N까지 순서대로 선택한다.
7. 위 점화식을 사용하여 D[i][j]를 갱신한다.
8. 모든 반복이 끝나면 D[i][j] 배열에는 모든 쌍 i와 j 사이의 최단 거리가 저장된다.

시간복잡도

---

• $O(n^3)$

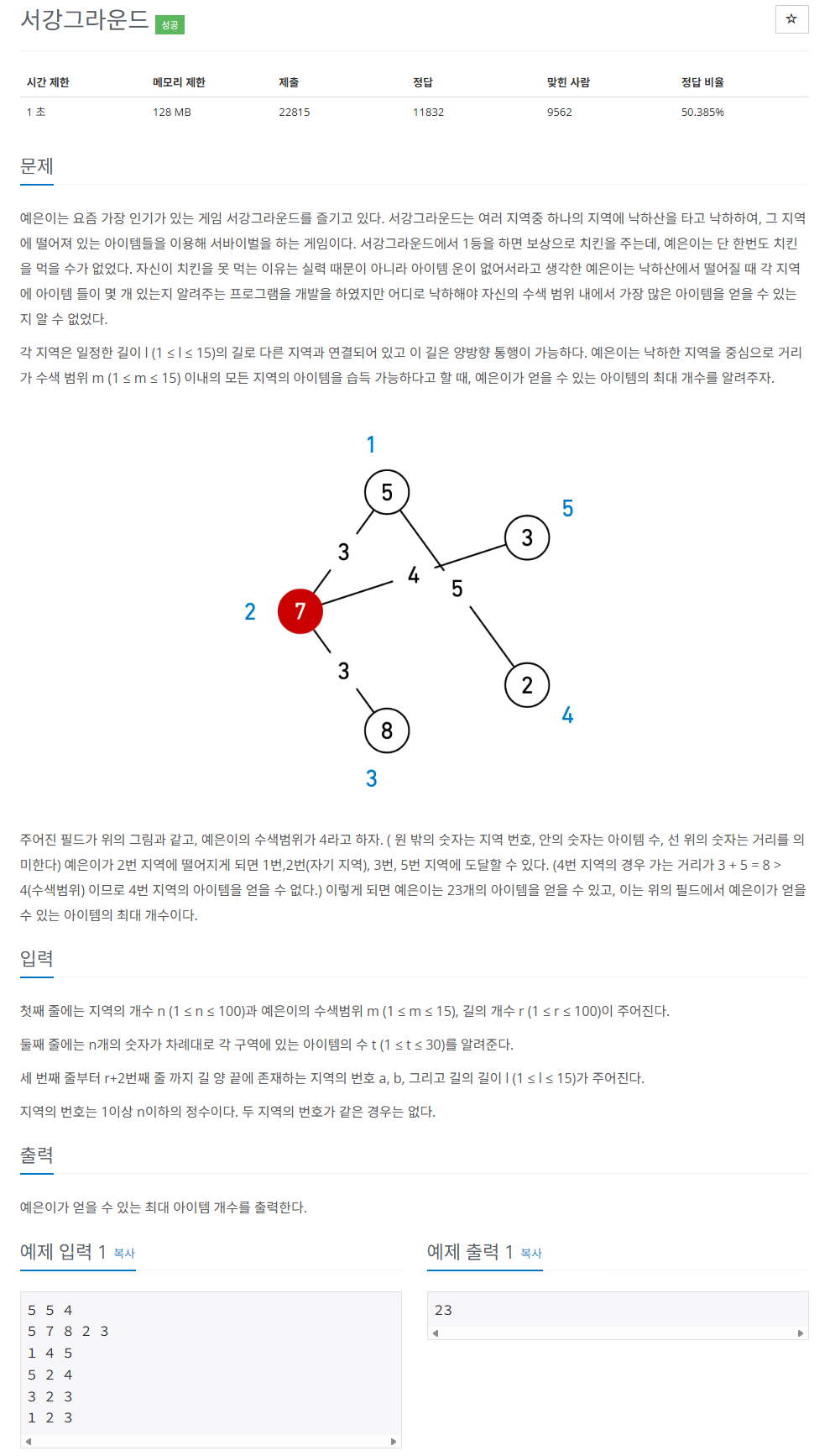
백준 14938번 : 서강 그라운드

---

#include <iostream>
#include <vector>
#define INT_MAX 1000000

int main()
{
    std::ios_base::sync_with_stdio(false);
    std::cin.tie(nullptr);
    std::cout.tie(nullptr);

    int n, m, r;
    std::cin >> n >> m >> r;

    std::vector graph(n, std::vector<int>(n));
    std::vector item_num(n, 0);

    for (int i = 0; i < n; i++)
    {
        std::fill(graph[i].begin(), graph[i].end(), INT_MAX);
        graph[i][i] = 0;
    }
    
    for (int i = 0; i < n; i++)
    {
        std::cin >> item_num[i];
    }

    for (int i = 0; i < r; i++)
    {
        int start, end, cost;
        std::cin >> start >> end >> cost;
        start--;
        end--;
        graph[start][end] = cost;
        graph[end][start] = cost;
    }

    for (int k = 0; k < n; k++)
    {
        for (int i = 0; i < n; i++)
        {
            for (int j = 0; j < n; j++)
            {
                graph[i][j] = std::min(graph[i][j], graph[i][k] + graph[k][j]);
            }
        }
    }

    int ans = 0;
    for (int i = 0; i < n; i++)
    {
        int temp_ans = 0;
        for (int j = 0; j < n; j++)
        {
            if (graph[i][j] <= m)
            {
                temp_ans += item_num[j];
            }
        }
        ans = std::max(ans, temp_ans);
    }
    
    std::cout << ans;
    
    return 0;
}