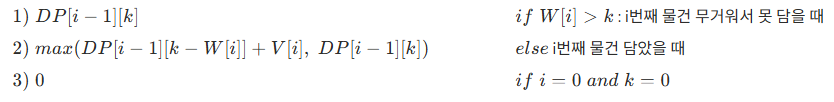0/1 배낭 문제 Knapsack Problem

이 글은 제 개인적인 공부를 위해 작성한 글입니다.
틀린 내용이 있을 수 있고, 피드백은 환영합니다.

개요

---

배낭 문제는 조합 최적화의 고전적인 문제로, 한정된 용량의 배낭에 최대의 가치를 갖도록 문제를 담는 방법을 찾는 문제이다.

가령, 도둑이 보석 가게에 침입했는데 보석마다 무게와 가치가 다르고, 배낭의 무게 제한이 10KG라면 어떤 보석들을 담아야 가장 비싼 값을 받을 수 있을까? 라는 상황과 같다.

배낭 문제는 크게 두 가지로 나눌 수 있다.

1. 0/1 배낭 문제: 물건을 담거나 담지 않거나 하나만s 선택할 수 있는 경우이다. 동적 계획법으로 해결할 수 있다.
2. 분할 가능 배낭 문제 : 물건을 쪼개서 담을 수 있는 경우이다. 그리디 알고리즘으로 해결할 수 있다.

이 글에선 0/1 배낭 문제만 이야기해보자.

0/1 배낭 문제

---

W = 각 물건이 차지하는 무게, V = 각 물건의 가치

$(W_i,V_i)$의 무게와 가치를 가지는 N개의 물건이 있을 때, 최대 K무게까지 담을 수 있는 배낭의 최대 가치는?

1. $(W_1,V_1)$ 삽입

   $(K-W_1)$을 더 담을 수 있고 현재 가치는 $V_1$

   → $(W_1,V_1)$을 제외하고,

   최대 $(K-W_1)$ 무게까지 담을 수 있는 배낭의 최대 가치는?

2. $(W_2,V_2)$ 삽입

   $(K-W_1-W_2)$을 더 담을 수 있고 현재 가치는 $V_1+V_2$

   → $(W_1,V_1),(W_2,V_2)$을 제외하고,

   최대 $(K-W_1-W_2)$ 무게까지 담을 수 있는 배낭의 최대 가치는?

즉, 6KG 까지 넣을 수 있는 배낭의 최대 가치는 3KG을 넣었을 때 + 3KG 까지 넣을 수 있는 배낭의 최대 가치와 동일하다.

큰 문제가 작은 문제들로 나뉠 수 있고, 작은 문제들이 큰 문제의 답이 된다.

상황을 쪼개어 생각해보면 이해하기 좀 더 쉽다.

1. 물건의 무게가 최대 배낭 무게를 초과할 때

   물건을 배낭에 넣을 수 없다. 최대 가치는 이전의 최대 가치로 유지

2. 물건의 무게가 최대 배낭 무게를 초과하지 않을 때

   1. 넣지 않는다.

      물건을 넣지 않는 것은 똑같기 때문에 최대 가치는 이전의 최대 가치로 유지

   2. 넣는다. 최대 K 무게까지 담을 수 있는 배낭에 W를 넣었을 때, K - W개를 더 담을 수 있다.

      최대 K - W 무게까지 담을 수 있는 배낭의 최대 가치는?

점화식

---

DP[i][k] = 최대 K 무게까지 담을 수 있고, 1 ~ i번째 물건까지 고려했을 때, 최대 가치의 합

백준 12865번 평범한 배낭

---

https://www.acmicpc.net/problem/12865

#include <iostream>
#include <vector>
#include <algorithm>

int DP[101][100001] = {};

int main()
{
    std::ios_base::sync_with_stdio(false);
    std::cin.tie(nullptr);
    std::cout.tie(nullptr);
    
    int n, k;
    std::cin >> n >> k;
    
    std::vector<int> Weight(n + 1);
    std::vector<int> Value(n + 1);
    
    for (int i = 1; i <= n; i++)
    {
        std::cin >> Weight[i] >> Value[i];
    }
    
    for (int limit = 1; limit <= k; limit++)
    {
        for (int i = 1; i <= n; i++)
        {
            if (Weight[i] > limit)
            {
                DP[i][limit] = DP[i - 1][limit];
            }
            else
            {
                DP[i][limit] = std::max(DP[i - 1][limit], DP[i - 1][limit - Weight[i]] + Value[i]);
            }
        }
    }
    
    std::cout << DP[n][k];
    
    return 0;
}